The Jones “Rule of 86” was devised in 1946 by C.H. Jones, a scientist and educator at the University of Vermont.  

Originally it was incorporated into a poem that taught several best management practices in a humorous way (see “The maple rule of eighty-six”, reprinted on pages 18-19 of the December 1967 edition of the “National Maple Digest” and pages 129-132 of Maple Sugarin’ in Vermont, by Betty Ann Lockard 2008).  

The gist of the rule is that if one divides 86 by the sugar content of sap, you can estimate the amount of sap required to produce a gallon of syrup.  Thus:

S = 86/X   and W = S -1

Where: S = the initial volume of sap (or concentrate) required to produce 1 gallon of syrup

X = the starting sap (or concentrate) sugar concentration in °Brix.

W = the amount of water to be boiled off to produce 1 gallon of syrup

(Nomenclature from the North American Maple Producers Manual, Second Edition, 2006)

Thus it is easily seen that an average sap sugar concentration of 2°Brix would require 43 gallons of sap to produce 1 gallon of syrup, or a sap:syrup ratio of close to 40:1.

At the time it was devised, the rule was intended to serve as a simple to calculate (pocket calculators and Smart Phones hadn’t been invented yet) and easy to remember tool for maple producers to estimate the number of gallons of sap required to make a gallon of syrup at a given sap sugar content.  

One must also realize that the standard legal syrup density at the time was 65.5°Brix, and that given the existing technology, this guideline was only used in a fairly low and narrow range of sap sugar concentration.

Fast forward to the present day when concentration by reverse osmosis is common, and the value and difference in sap (or concentrate) sugar content can be fairly high, and sap and syrup prices are relatively high, and we should therefore not be surprised to find that the old “rule” doesn’t seem to hold up any longer.  

Those who spend a little time thinking about this (and those who often buy or sell concentrate) realize that if you use the Rule of 86 on highly concentrated sap, things just fall apart.  An extreme example helps illustrate this point quickly and clearly.    

As above, the “Rule of 86” states:

S = 86/X

If we assume a sap sugar concentration equal to syrup density in 1946 of 65.5°Brix, we end up with:

S = 86/65.5 = 1.31

Meaning that using the “Rule of 86”, it would take 1.31 gallons of sap at 65.5°Brix to make 1 gallon of syrup at 65.5°Brix!  

What’s going on?  That answer just doesn’t make any sense.

For starters, one of the reasons the “rule” doesn’t always work well is that the standards for density of maple syrup have changed since 1946.  For many places, minimum syrup density is 66.0°Brix.  In some states, the minimum density of syrup is 66.9°Brix.  

Surprisingly, even these small apparent differences at the syrup level can have large effects on the amount of sap required at a given sap sugar content.

Secondly, the “Rule of 86” was never meant to calculate the precise amount of sap needed.  It’ll get you in the ballpark, which for the sugar concentrations of raw sap it was originally used for, turned out to be good enough.   

Finally, the original calculations actually produced a “Rule of 86.26”, but given the intended usage and range of sap sugar concentration at the time, rounding to 86 seemed close enough.

Given our increasingly powerful Reverse Osmosis machines, the resultant high concentrate sugar levels attainable today (up to 40°Brix!), as well as the vast quantities of sap and concentrate being sold in the industry, along with the current high price of syrup, a more precise quantification tool is necessary in many cases.

Without delving too deeply into the chemistry of sugar solutions or the math, a much closer approximation of the amount of sap (or concentrate) needed to produce one gallon of syrup at 66.0°Brix can be obtained using a slight alteration to the “rule.”

S = 87.1/X-0.32   and   W = S-1

Note: Keep in mind the proper mathematical order of operations (divide first, then subtract).

For syrup at a density 66.9°Brix, the formula needs to be slightly adjusted again.

S = 88.2/X-0.32    and   W = S-1

Both of these formulas are still approximations, but are relatively easy to calculate and get us much closer to the current true value than the original “Jones Rule of 86.”

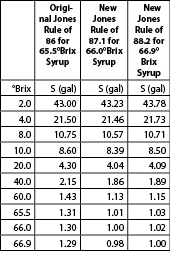
Some examples are given in the Table below.  Values are provided in S (volume of sap required to produce one gallon of syrup) in gallons of sap at a given Brix value.  

So why does this matter?  

As an example; if a sugarmaker has 100 gallons of 2% sap, based on the original Jones Rule, that sugarmaker would calculate they should be able to make 2.33 gallons of syrup.   

However, the original Jones Rule tends to overestimate when it comes to sap.  According to the updated Jones rule, for a state with 66.9°Brix as a minimum, the sugarmaker can expect to produce 2.28 gallons of syrup.  

The 0.05 gallons of syrup difference, while seemingly small, represents about a 2.1% decrease when calculating syrup production, which may be quite significant to the bottom-line when large quantities of sap are involved.  

The relationship changes for higher sap sugar concentrations  – the original Rule underestimates production of syrup for concentrate.  

Buyers and sellers of sap and concentrate may wish to adjust accordingly.  

Of course, all of this also presumes that the observed measurements of sap, concentrate, and syrup sugar content are both accurate and precise.  

That however, is another lesson for next time.

December 2013